현의 진동수
전편에서 피아노가 다른 건반악기로부터 구별되는 가장 큰 특징 중 하나가 해머라고 했었다. 이 해머는 건반이 눌림과 동시에 현을 강하게 타격하고 후퇴함으로써 소리를 만들어내는데, 이번 편에서는 과연 해머가 현을 때리게 될 때, 그리고 때리고 난 뒤 피아노줄에 유도되는 파동의 특성을 이해하고 이를 통해 피아노줄의 특징과 그로 인한 피아노 소리의 특성 등을 이야기하고자 한다. 아, 논의를 시작하기에 앞서서 이 글에서는 피아노줄을 현(絃)이라는 단음절 단어로 간단하게 표현하고자 하니 오해 없기를 바란다.

▴ 그랜드 피아노 건반에 매여 있는 피아노줄의 배치 및 구성1
해머가 현을 위로 강하게 때려 올리면 현에 위쪽으로 변형(x-ε)이 생기고, 해머에도 변형(ε)이 생긴다는 것을 전편에서 언급했었다. 그런데 물리학에서 현은 대체로 미소한 단위의 점 성분들이 장력(tension)에 의해 서로 1차원적으로 연결되어 있는 것으로 인식된다. 따라서 아래 그림과 같이 변형된 현을 확대해서 살펴본다면, 변형된 부분의 점 성분들은 모두 휘어진 현의 접선의 방향으로 장력을 받게 된다고 기술할 수 있다.

▴ 변형된 현에 작용하는 장력
변형된 현에 작용하는 장력들을 모두 더하면 어떻게 될까? 힘은 벡터(vector)이므로 벡터합을 잘 생각해보자. 현이 수평한 방향으로 놓여있다는 가정하에서 계산할 때, 우선 장력을 수평방향 장력(T∥)과 수직방향 장력(T⊥)으로 나눠서 생각할 수 있다. 그렇다면 장력의 합은 수평방향 장력들의 합과 수직방향 장력들의 합과 같을 것인데, 다행히도(?) 수평방향 장력의 합은 0이 된다. 그러니 수직방향으로 현을 퉁길 때 현이 왼쪽이나 오른쪽으로 움직이지 않는 것이다. 수직방향 장력들의 힘을 다 합치면 (이상적으로는) -(F-σ)가 된다. 즉, 해머가 현을 변형시킬 때 밀어붙인 힘과 크기는 같으나 반대는 방향인 장력이 변형된 현에 형성되어 해머를 아래 방향으로 짓누르는 것이다. 이것은 뉴턴의 제3법칙인 작용-반작용의 법칙을 이해하면 너무나 쉽게 이해할 수 있는 부분이다.

▴ 변형된 현에 작용하는 장력 성분들과 합
따라서 윗방향으로 변형된 현에는 아랫방향으로 작용하는 힘이 생기기 때문에 위로 퉁겨진 현은 제자리를 지향하는 듯 아래로 향하게 된다. 이처럼 원래 자리로 돌아가고자 하는 힘을 복원력(restoring force)이라고 부르며, 용수철이 왔다갔다하는 것도 이와 같은 복원력 때문이다. 아무튼 이 복원력에 의해 현은 제자리로 돌아가려고 한다. 그러나 뉴턴의 제1법칙이 현을 가만 놔두지 않는다. 바로 관성(慣性, inertia) 때문에 현이 제자리에서 멈추지 못하고 그대로 아래로 더 나아가 휘어지게 되는 것이다.
그러면 현이 아래 방향으로 변형된 것이고 위에서 펼친 논리에 따르면 이제는 복원력이 윗방향으로 작용하게 된다. 따라서 현은 위로 움직여 원래 자리를 되찾으려고 한다. 하지만, 역시 관성 때문에 현은 제자리를 지나쳐 위로 휘어지게 된다. 현이 에너지를 잃지 않는다면 이 왔다 갔다 진동은 무한히 지속될 것인데, 이 운동이 바로 현의 파동이다. 해머가 현을 때리게 되면 현이 진동하게 된다는 사실은 누구나가 잘 알고 있지만 이렇게 물리학적으로 해석할 수 있는 것이다.
그런데 현은 당연하게도 양쪽 끝이 고정되어 있다. 따라서 해머의 타현으로 인해 형성된 파동은 현을 따라 전파되다가 양쪽 끝에서 반사된다. 그리고 이 파동은 이전의 파동과 겹쳐져서 간섭을 일으키고... 가만, 이거 어디서 들어본 내용 아닌가? 바로 2편에서 정상파를 언급할 때 나온 이야기이다. 즉, 해머가 현을 때리게 되면 현에는 정상파가 형성된다는 것이 결론이다.
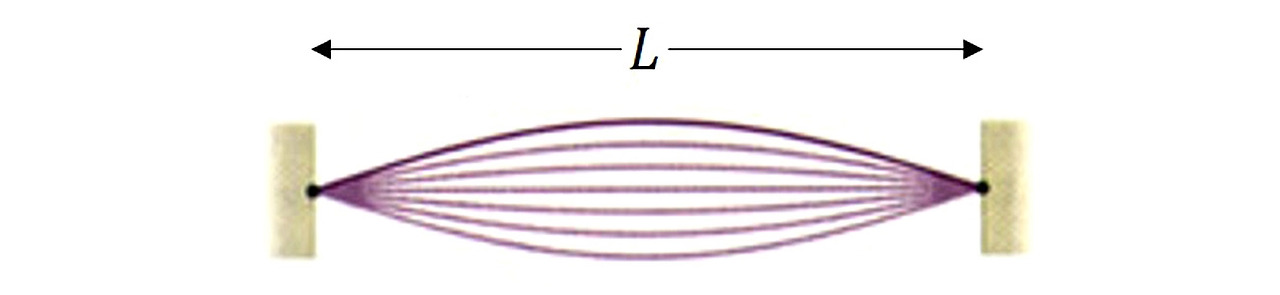
▴ 정상파가 형성된 현
정상파도 파동의 일종이며 파동은 파동의 방정식을 만족시키는 해(解)이다. 1차원 현에 수직 방향으로 진동하는 파동을 역학적으로 계산하면 다음과 같은 미분 방정식의 꼴을 얻을 수 있다.
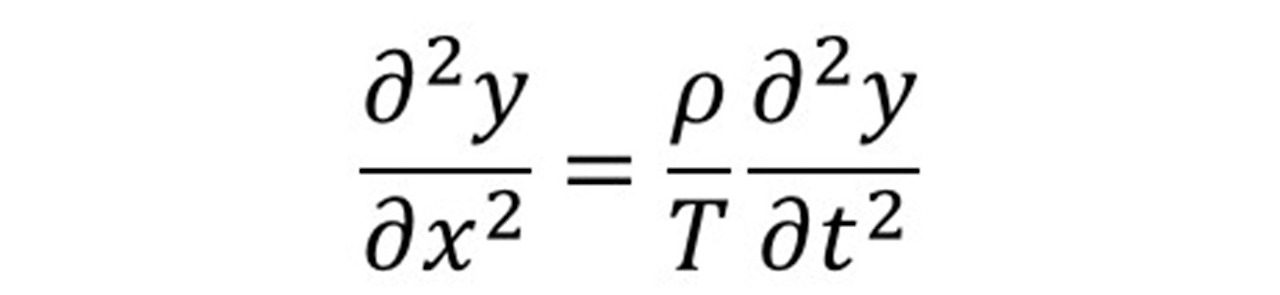
▴ 이상적인 현의 방정식. (ρ: 선밀도(단위 길이당 현의 질량), T: 장력)
한편 속도 v로 진행하는 파동은 일반적으로 y(x,t) = A sin[2πf(x-vt)] 와 같은 사인함수로 표현할 수 있으므로 이 식을 위 미분 방정식에 대입하면 다음과 같은 결론을 얻을 수 있다.
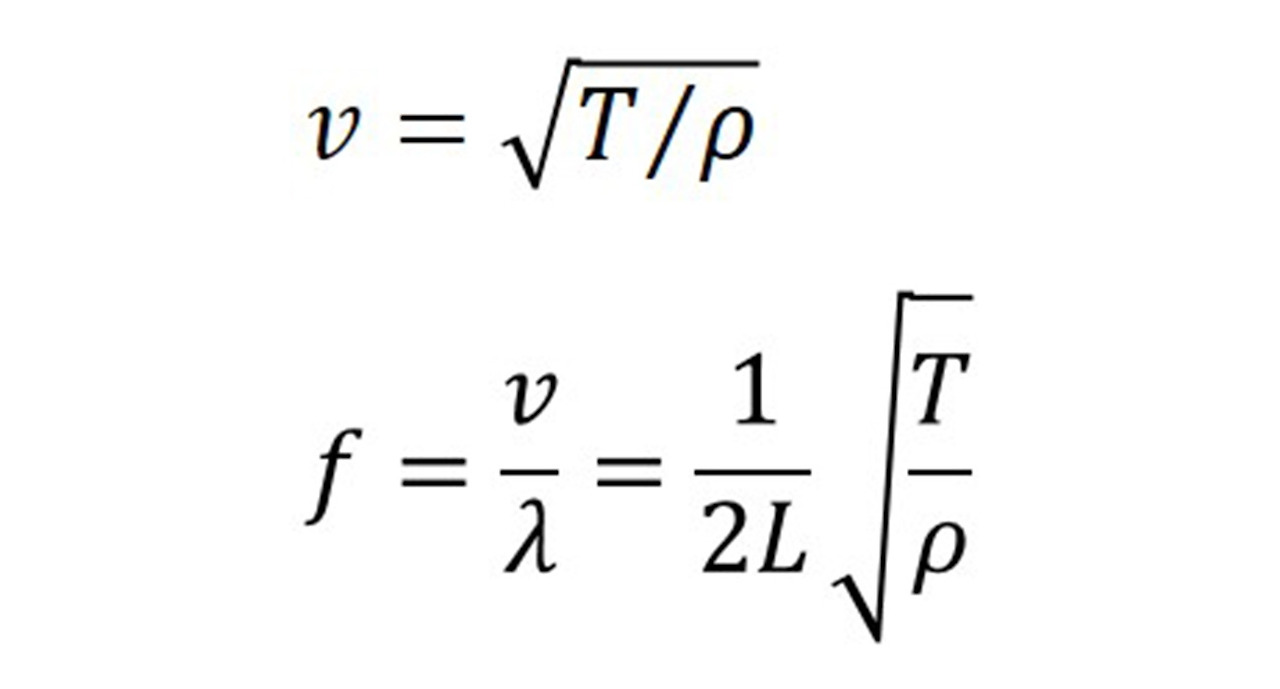
▴ 현에 유도된 파동의 속도(v)와 진동수(f)의 해
현에 유도된 파동의 속도와 진동수의 표현을 자세히 살펴보면 세 가지 인자가 이들 값에 영향을 주는 것을 알 수 있다.
⦁ L : 현의 길이
⦁ ρ : 현의 선밀도
⦁ T : 현에 걸리는 장력
그리고 각 인자 값이 증가하거나 감소하면 그에 따라 파동의 진동수가 다음과 같이 변하게 되는 것을 알 수 있다. (+: 진동수 증가 / -: 진동수 감소)
| L | ρ | T | |
| 값 증가 | - | - | + |
| 값 감소 | + | + | - |
현의 진동수가 소리의 무엇과 관계된 인자였는지 기억이 나지 않는다면 1편을 다시 참고하라. 현의 진동수는 소리의 음높이와 관련된 것이었다. 진동수가 높아질수록 높은 음이며 진동수가 낮아질수록 낮은 음인 것이다. 따라서 물리학적으로 구한 저 진동수 식에 따르면 피아노의 음정은 현의 길이, 선밀도, 그리고 장력에 의해 제어되어야 할 것이다. 실제로 그럴까? 물론이지. 물리학은 거짓말을 잘 못한다.
피아노 내부 사진을 다시 한 번 기억해보면, 건반이 내는 음높이가 높을수록 현의 길이는 짧아지고 반대로 음높이가 낮을수록 현의 길이가 길어진다. 이것은 정확하게 위에서 살펴본 현의 길이(L)와 진동수(f) 사이 관계에 들어맞으며, 업 라이트 피아노든 그랜드 피아노든 이 법칙을 눈으로 직접 확인해볼 수 있다. 특히 그랜드 피아노의 경우 베이스 영역의 건반은 낮은 음을 내야 하니까 진동수를 낮추기 위해 현의 길이가 길어져야 하므로 대체로 한쪽이 길게 삐져나와 있는 외형을 갖추게 되는 것이다. 그런데 여기에 문제가 하나 있다. 대체로 가온다(C5)2음을 내는 건반에 연결된 줄의 길이는 대략 0.62 m 이다. 따라서 현의 길이를 늘리는 것만으로 진동수를 낮추려고 한다면 일반적인 피아노의 가장 낮은 음(A0)을 내는 건반에는 무려 6 m 길이의 현이 연결되어 있어야만 한다. 연주를 하기 위한 악기 치고 6 m 는 너무 길다. 무슨 방법이 없을까? 이럴 때는 L 말고 다른 인자를 제어하면 된다. 바로 선밀도(ρ)이다.
어떻게 하면 현의 선밀도를 높일 수 있을까? 가장 간단한 것은 현의 굵기를 다르게 하는 것이다. 굵은 현은 부피가 크단 뜻이고 동일한 밀도 하에서 큰 부피는 곧 큰 질량을 의미하니 굵은 현은 단위 길이당 질량이 커질 수밖에 없다.
| 음정 | 진동수 (Hz) | 현의 굵기 (mm) |
| C8 | 4186 | 0.76 |
| C7 | 2093 | 0.81 |
| C6 | 1047 | 0.86 |
| C5 | 523 | 0.95 |
| A4 | 440 | 0.95 |
| C4 | 262 | 1.00 |
위에서 알 수 있듯이 음높이가 낮아질수록 현의 굵기가 점차 굵어지는 것을 알 수 있다. 그러나 여기에도 한계가 있다. 가장 낮은 음인 A0의 진동수가 28 Hz인데, 이를 만족시키려면 현의 굵기가 3 mm 이상 되어야 한다. 그런데 과연 굵기가 3 mm 이상인 현을 악기 줄이라고 표현할 수 있을까? 그것은 가는 금속 막대기가 될 것이다. 그리고 가는 금속 막대기는 이상적인 현과는 거리가 멀기 때문에3 여기서 생성되는 파동은 앞에서 간단하게 살펴본 방식을 따르지 않게 될 것이며 그 결과 기대했던 음정과는 전혀 다른 엉뚱한 소리가 둔탁하게 날 것이 뻔하다. 따라서 다른 방법이 필요한데, 이를 극복하기 위해 중심현에 또다른 현을 주변에 감는 방식이 활용되었다. 기타를 쳐본 사람들은 대번에 알아차릴 텐데, 가장 가는 기타줄은 단선이지만, 가장 두꺼운 기타줄은 압축해놓은 용수철마냥 뭔가 칭칭 감겨 있는 줄인 것을 기억하고 있을 것이다. 피아노줄도 그렇다는 것이다. 즉, 아래 그림과 같이 다른 줄을 중심현 주변으로 돌돌 감아 피아노줄을 만드는 것이다.

▴ 낮은음 표현을 위한 감은 현
| 음정 | 진동수 (Hz) | 현의 굵기 (mm) | 감은 줄의 굵기 (mm) |
| A3 | 220 | 1.0 | 0.0 |
| C3 | 131 | 0.9 | 0.3 |
| A2 | 110 | 0.9 | 0.5 |
| C2 | 65 | 1.0 | 1.0 |
| A1 | 55 | 1.1 | 1.0 |
| C1 | 33 | 1.4 | 1.8 |
| A0 | 28 | 1.6 | 2.0 |
표에서도 확인할 수 있듯이 음정이 낮아질 수록 현의 굵기가 조금씩 굵어짐과 동시에 감은 줄의 굵기 역시 굵어지는 것을 알 수 있다. 이렇게 줄을 감으면 중심 현의 거동에 큰 제약을 주지 않은 채 선밀도를 효과적으로 늘릴 수 있게 된다. 굳이 예를 들자면, 마른 사람이 두터운 패딩을 입는 것과 마찬 가지이다. 겉에서 보기엔 뚱뚱한 사람과 체형이 비슷하지만 움직임은 패딩 없이 뛰어다닐 때와 큰 차이가 없지 않은가! 아무튼 이렇게 감은 줄을 이용해서 현의 선밀도를 효과적으로 제어한 덕분에 베이스 영역 건반에 연결된 현의 길이가 무작정 길어지는 걱정을 하지 않아도 되었다. 그 결과 연주회용 그랜드 피아노의 사이즈가 3 m 정도를 넘지 않을 수 있게 되었고 외형이 지나치게 길어져 괴상하게 보이는 걱정도 덜 수 있었다.
그렇다면 마지막 다른 인자인 장력은 음높이에 어떻게 영향을 줄까? 장력은 현이 팽팽하게 잡아당겨진 정도라고 볼 수 있는데, 피아노 내부를 잘 들여보면 알 수 있지만 각 현은 모두 양쪽의 핀에 의해 고정되어 있는데, 건반쪽에 있는 핀을 튜닝 핀(tuning pin)이라고 하고, 반대편에 고정되어 있는 핀을 히치 핀(hitch pin)이라고 한다. 그런데 튜닝 핀이라고 이름이 붙은 이유가 뭘까? 이 핀은 나사처럼 되어 있어서 렌치를 이용하여 쉽게 시계 방향 혹은 반시계 방향으로 돌릴 수가 있다. 튜닝 핀에 현이 감겨 있는 형태를 자세히 보면 마치 기타 줄이 매여 있는 튜닝 펙(tuning peg)을 보는 것과 유사하게 돌돌 감겨 있는데, 튜닝 핀을 한쪽 방향으로 돌리면 줄이 더 감기게 되고 반대 방향으로 돌리면 줄이 풀리게 된다. 줄이 더 감기게 되면 핀 사이에 있는 줄은 더 팽팽하게 잡아당겨지므로 현에 인가된 장력은 증가하게 된다. 따라서 현에 유도된 정상파의 진동수가 증가하게 된다. 바로 이러한 방식으로 장력이 피아노 음높이에 영향을 주는 것이다.
장력을 이용한 음높이 조절은 대개 피아노 조율사가 집이나 연주회장을 방문했을 때 확인할 수 있다. 조율사는 손상된 현을 교체하고 해머 구조의 이상을 점검함과 동시에 렌치를 이용하여 튜닝 핀을 조였다 풂으로써 원래 내야 하는 소리를 벗어난 건반 소리를 바로잡는데, 이 과정이 곧 장력을 제어하여 음정을 맞추는 것이다.
파동의 물리학
그렇다면 파동이란 무엇인가? 파동이란 '매질을 통해 운동이나 에너지가 전달되는 현상'을 일컫는다. 파동이 전파될 때 매질은 움직이지 않는다는 것은 기본적인 상식으로 잘 알려져 있다. 즉 바다 한가운데서 파도가 일렁이지만 그 위에 떠 있는 부표(浮標)는 수직 방향으로 넘실거리기만 할 뿐 수평 방향으로는 움직이지는 않는다는 것이다.
세상에는 참으로 다양한 파동들이 있다. 그러나 이러한 파동들은 모두 공통적인 특성을 공유하고 있으며 이러한 것들을 물리량으로 정의하면 아주 간단한(?) 수학식으로 나타낼 수 있다. 소위 파동의 요소들이라 불리는 것에는 다음과 같은 것들이 있다.
⦁ 진폭(振幅, amplitude) : 진동 중심에서 최대 변위의 크기 (A)
⦁ 파장(波長, wavelength) : 같은 변위(위상)을 가진 서로 이웃한 두 점 사이의 거리 (λ)
⦁ 주기(週期, period) : 매질의 한 점이 1회 진동하는데 걸린 시간 (T)
⦁ 진동수(振動數, frequency) : 파동 전파시 매질의 한 점이 1초 동안 진동한 횟수 (f). 참고로 진동수는 주기의 역수이다. (f = 1/T)
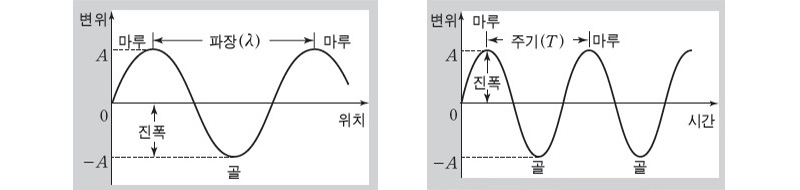
▴ 파동의 요소들
이러한 파동의 요소들을 고려하여 위의 그림과 같은 단순한 파동을 수학식으로 표현하면 다음과 같다.
파동은 중첩(重疊, superposition)과 관련된 여러 가지 재미있는 성질을 나타낸다. 선형 조합(linear combination)이라는 어려운 용어를 사용하지 않아도 이 중첩의 원리는 간단히 설명할 수 있는데, 각기 진행하던 파동들이 서로 만나게 되면 겹쳐지는 지역에서 파동은 위상이 단순히 더해질 뿐 각 파동의 고유한 속성이 변하지 않는다는 것이다. 아래 그림처럼 서로 마주오던 파동은 서로 만났다고 해서 부서지거나 합체하는 것이 아니며 만남의 시간이 끝나면 서로 쿨하게 헤어지게 된다. 그런데 이렇게 헤어질 때 자기 자신의 속성이 변하지는 않으므로 처음에 왔던 그 모습 그대로 떠나가게 된다. (왠지 각박한 현대 사회의 이별을 보는 것은 기분 탓이다.)
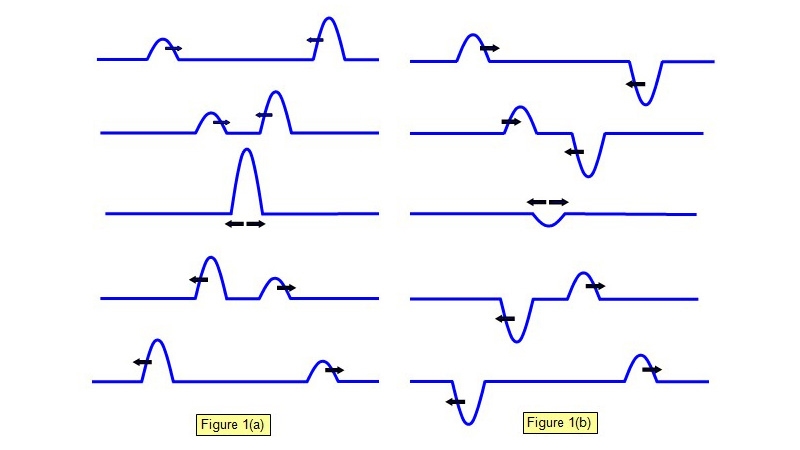
▴ 파동의 중첩을 나타낸 그림
위에서는 진행이 매우 짧은 일종의 펄스(pulse)파의 중첩을 나타낸 것이었다. 그렇다면 연속적으로 이어지는 파동이 겹치면 어떻게 되나? 이 경우 우리는 새로운 파동을 얻게 되며 이를 간섭(干涉, interference)이라고 한다. 그런데 왼쪽 그림처럼 서로 같은 위상의 파동이 만나게 되면 진폭은 커지게 되는데 이와 같은 간섭 형태를 보강 간섭(補强干涉, constructive interference)이라고 한다. 반대로 오른쪽 그림처럼 서로 다른 위상의 파동이 만나게 되면 진폭은 작아지게 되는데 이를 상쇄 간섭(相殺干涉, destructive interference)이라고 한다. 극단적으로 말하면 이런 현상도 발생한다: 진폭과 진동수가 똑같은 두 파동이 간섭을 일으키면 진폭이 두 배가 된 파동이 형성된다. 그러나 동일한 파동이되 위상이 반대이면 간섭의 결과 완전히 파동이 없어진 것처럼 느껴진다. 후자의 경우 가수들의 라이브 실력을 알아보기 위해 사람들이 흔히 행하는 MR 제거의 원리인데, 즉 반주 음원의 위상을 죄다 180도 바꾸어 놓고나서 가수의 라이브 음원과 중첩을 시킨다. 그러면 상쇄 간섭이 일어나서 라이브 음원에서 반주에 해당하는 소리의 파동은 죄다 없어진 것처럼 되어 버리게 된다! 이러한 중첩과 무관한 가수의 목소리만 살아남은 결과 가수는 대중들에게 찬탄을 혹은 비난을 받게 되는 것이다.

▴ 보강 간섭과 상쇄 간섭, 그리고 일반적인 사인 파동의 간섭
정상파
그런데 위에서 언급한 파동들은 모두 끝이 없이 진행하는 파동들이다. 즉, 한번 형성된 파동은 (에너지의 감쇄가 없다고 가정할 때) 지구 끝, 아니 우주 끝까지 전달된다고 가정하는 것이다. 하지만 세상에 이런 파동들만 있는 것은 아니다. 만일 파동에게 처음과 끝이 주어지게 된다면 어떤 일이 발생할까? 예를 들어 출렁이는 밧줄이 있다고 할 때 그 밧줄의 양끝을 막대기에 묶어버린다고 해보자. 이처럼 양쪽 끝이 고정 혹은 한정된 매질에서의 파동인 경우, 고정된 점에서 파동이 반사하게 된다. 그런데 연속적인 파동이라면 이렇게 반사하여 되돌아가는 파동은 지속적으로 밀려 들어오는 파동과 중첩되어 간섭을 일으키게 된다. 그 결과 마치 전파되지 않고 가만히 멈춰 서 있는 것 같은 파동이 형성된다.¹
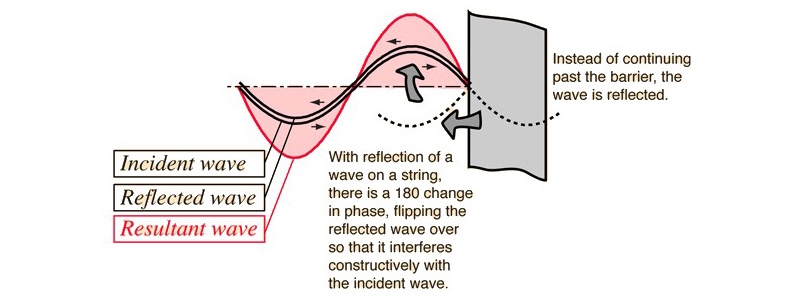
▴ 정상파의 형성
앞서 언급한 간섭 원리를 떠올린다면, 정상파의 진폭은 보강 간섭으로 인해 본래의 파동보다 더 큰 것임을 바로 알아차릴 수 있을 것이다. 정상파의 가장 극적인 예가 바로 1940년에 붕괴한 미국의 타코마(Tacoma) 다리이다. 다소 충격적인 영상이기도 한데, 당시 강에 불던 바람이 현수교(懸垂橋)인 타코마 다리에 정상파를 형성해 놓았고, 지속적인 바람에 의해 다리에 만들어진 파동이 계속 보강 간섭을 일으켜 진폭이 커지다가 결국 다리의 기계적 한계를 넘어서는 바람에 다리를 붕괴시키기에 이른 것이다.
▴ 타코마 다리의 붕괴 장면을 찍은 동영상
그런데 이 영상을 자세히 보면 중간에 연구자가 다리의 중앙 부분을 지그재그로 유유히(?) 걸어가는 것을 확인할 수 있는데 해당 지점은 크게 출렁이지 않는 부분으로 사람이 흔들리지 않고 걸어갈 수 있었던 지점이다. 실제로 정상파가 형성되면 자신의 파장의 반정수배 및 정수배, 곧 1/2배, 1배, 3/2배... 에 해당하는 지점은 정말로 가만히 멈춰 서 있는데 이를 마디(node)라고 한다. 아래 그림에서 보면 양쪽을 고정시킨 실에서 발생한 정상파의 경우 다양한 정상파마다 점의 형태로 마디가 형성되어 있는 것을 확인할 수 있다. 타코마 다리에 형성된 정상파에는 마디가 평판 위의 곡선을 따라 형성되어 있었고, 연구자는 그 위를 유유히(?) 걸어나갈 수 있었던 것이다.
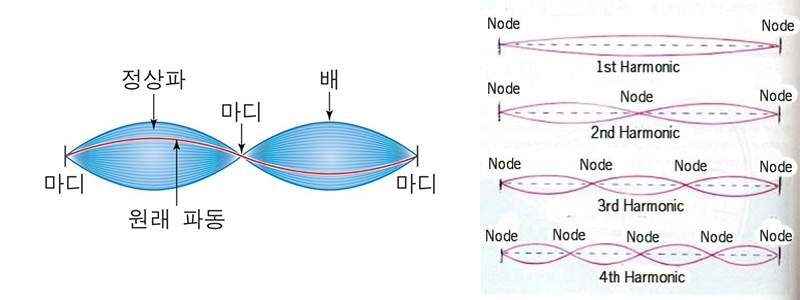
▴ 정상파에서 발견되는 마디
양쪽을 고정시킨 줄에 어떠한 이유로 인해 정상파가 형성되었다고 생각해 보자. 파동은 에너지를 전달하는 현상이라고 했으나 정상파는 위와 같은 제한 조건에 갇혀 더 이상 확산되지 못하는 파동이므로 에너지를 계속 보유하게 된다. 따라서 아주 이상적인 실이 진공 중에서 떤다면,² 그 정상파는 세상 끝날 때까지 그 자리에서 영원히 떨게 될 것이다. 그러나 현실 세계에서는 이런 일이 발생하지 않으며, 무엇보다도 가장 중요한 것은 정상파 주변으로 충만하게 공기가 존재한다는 것이다. 정상파로 인해 요동치는 실은 주변에 있는 공기를 자신과 같은 진동수로 떨게 만드는데 이를 통해 공기에도 정상파를 유도한다. 어떻게? 실이 바깥으로 밀리면 공기도 바깥으로 밀어내어 갑자기 공기의 밀도가 높아진다. 실이 이제 안쪽으로 당겨지게 되면 공기도 안쪽으로 당겨내어 이제 공기의 밀도는 낮아진다. 즉, 공기의 밀도가 높아졌다 낮아졌다를 반복하게 되는 것이다. 이것은 횡파(橫波, transverse wave)인 실의 떨림과는 전혀 다른 형태의 파동인 종파(縱波, longitudinal wave)이다. 아무튼 실의 떨림은 공기의 떨림으로 전이되었으므로 정상파의 에너지는 작아지게 되는 대신에 에너지의 상당수가 공기를 통해 이제 퍼져 나가기 시작한다.
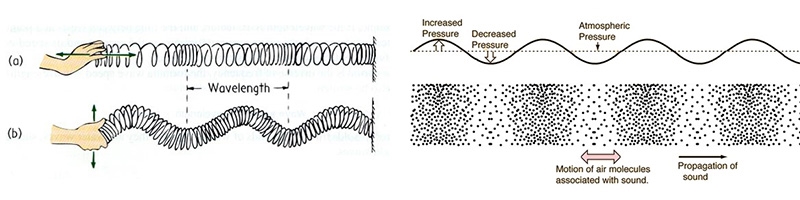
▴ 소리는 종파이다.
이것이 악기 소리의 본질이다. 악기에 유도된 정상파가 공기에 전달되어 형성된 진동이 바로 악기의 소리가 되는 것이다. 그러니 악기 소리는 악기 고유의 떨림이 아니라 그로 인해 유도된 공기의 떨림이라는 사실을 기억해야만 한다! 그렇다면 이것을 전편에서 본 호른보스텔-작스 분류법에 맞춰 해석할 수 있을까?
⦁ 체명악기, 막명악기, 현명악기 : 물체의 진동이 주변 공기를 진동시켜 음파 생성.
⦁ 공명악기 : 연주 시에 악기로부터 공기의 진동이 직접 만들어짐.
⦁ 전명악기 : 전자 신호가 스피커에 도달하면 스피커의 진동판이 진동하고 이것이 스피커 주변의 공기를 진동시켜 음파 생성.
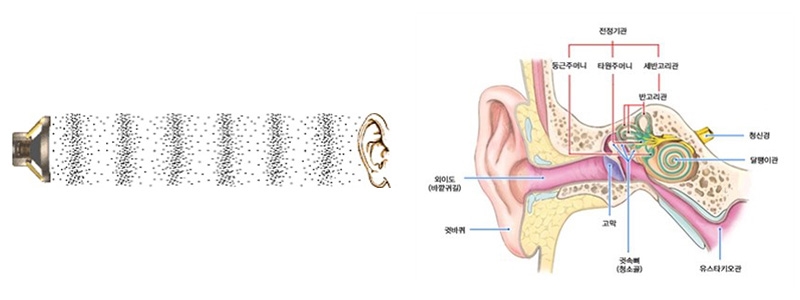
▴ 악기 소리의 전달
소리의 인식은 악기의 소리 발생 과정의 반대 과정으로 일어난다. 공기 중으로 발산되는 음파에 의해 귓속 고막이 진동하게 되고 이 진동이 청소골(聽小骨)에 의해 증폭되며 대뇌와 연결된 청신경을 자극하게 된다. 최종적으로 대뇌는 이 전기 신호를 인식하여 우리가 받아들이는 현상학적 개념인 '소리'를 인지하게 된다.
이제 악기의 소리가 악기 고유의 소리가 아닌 공기의 소리라는 것을 알게 된 독자들이라면 이제 더 이상 고체 물질만이 공기를 진동시키는 물질일 필요는 없다는 것을 이해할 수 있을 것이다. 세상 어떤 물질이더라도 최종적으로는 공기만 떨게 만들면 소리가 나는 것 아니겠는가? 그래서 이 세상에는 기존의 상식을 뒤엎는 다양한 실험적인 악기들이 개발되었다.
▴ 고체와 기체가 아닌 액체도 역시 물을 떨게 할 수 있다. 영상에서 연주되는 악기는 물 오르간이라고도 불리는 hydraulophone이다.
▴ 방전을 통해 발생된 전하 역시 공기를 떨게 할 수 있다. 이렇게 연주되는 악기를 통상적으로 plasmaphopne이라고 부른다.
소리의 3요소
그렇다면 우리가 배운 소리의 3요소를 이제 정상파라는 물리학적 개념에 맞추어 설명할 수 있을 것이다.
우선 음높이(pitch)를 생각해보자. 음높이란 사람이 인식하는 음파의 진동수로 정의가 된다. 즉 초당 파동이 몇 번 진동하는가에 따라 도레미파솔라시도가 결정된다고 이해하면 좋다. 단위는 헤르츠(Hz)인데 음높이의 기준이 되는 가(A)음의 진동수는 국제적으로 정의되길 440.00 Hz이다. 이보다 진동수가 높아지면 음높이는 올라가고, 진동수가 낮아지면 음높이는 내려가게 된다.
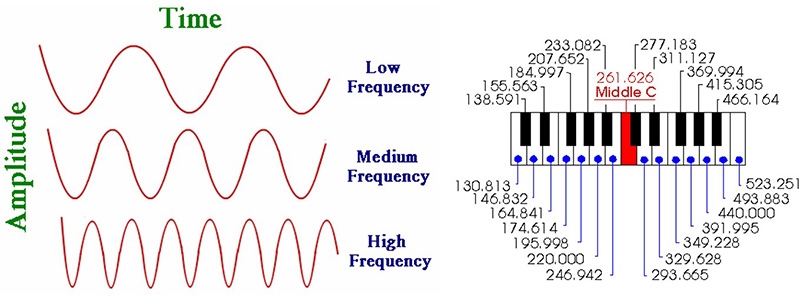
▴ 파동의 진동수와 음높이
그런데 음높이가 같더라도 사람은 모든 악기 소리를 동일하게 인식하지 않는다. 즉 피아노의 A음과 바이올린의 A음은 음높이는 같으나 전혀 동일하지 않은 소리이다. 이것을 음색 혹은 맵시(timbre)라고 부르는데 파동의 경우 기본 진동수는 같더라도 파형(波形, waveform)이 달라 나타나는 현상이다. 이를 이해하기 위해서는 위에서 언급한 파동의 간섭을 떠올려야 한다. 서로 다른 파동들이 합쳐지면 다른 파장을 가지는 파동을 만들 수 있는데, 이를 달리 말하면 어떤 파동은 서로 다른 기본 사인 파동들의 합으로 나타낼 수 있다는 말이다. 수학적으로 유식하게 말하면 세상 모든 파동은 서로 다른 진동수를 가지는 무수한 사인 파동들의 선형 조합으로 나타낼 수 있고,³ 이는 푸리에 변환(Fourier transformation)을 통해 해석 가능하다.
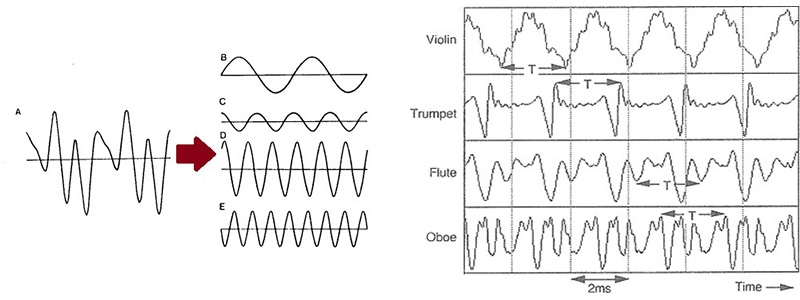
▴ 일반 파동의 분해 및 같은 음을 내는 악기들의 서로 다른 파형
마지막으로 세기(loudness)가 있다. 소리의 세기는 사람이 인식하는 음파의 세기로 결정된다. 여기서 중요한 것은 사람이 인식하는 음파의 세기라는 것이다. 통상적으로 사람이 간신히 들을 수 있는 세기인 1×1012 W/m2 를 기준으로 하여 상대적인 시끄러운 정도를 데시벨(dB)이라는 단위로 나타내는데 10배 시끄러울수록 dB이 10씩 올라간다. 예를 들어 지하철 소음에 해당하는 100 dB의 소리 세기는 진공 청소기 소음에 해당하는 80 dB의 소리 세기보다 100배 센 것이다.
이제 소리는 곧 악기로부터 유도된 물리학적인 파동이라는 사실을 정확하게 인식했으므로 본격적으로 피아노를 해부해보도록 하자. 그러나 이번 편에서 했던 방식으로, 즉 예술적으로가 아닌 물리학적으로 피아노를 해부해 볼 것이다. 여기서 본 것보다 더 많은 수식이 등장할 것이다.
-김성수
¹여기서는 고정단 반사만을 다룬다. 왜냐하면 후술하게 될 악기에서 발생하는 정상파의 경우 이러한 파동의 제한 조건은 모두 고정단 반사가 일어나는 조건이기 때문이다.
²이상적인 실의 조건 중 하나는 균일한 선밀도를 가져야 함과 동시에 완전히 탄성적이어서 굽힘이 발생할 때 전혀 저항이 없어야 한다. 물론 세상에 이런 실은 없다.
³이런 선형 조합이 자유롭게 가능한 이유는 파동 방정식(wave equation)을 만족시키는 해의 선형 조합 역시 파동 방적식의 해가 되기 때문이다. 참고로 파동 방정식은 이런 결론이 자연스럽게 도출되는 미분 방정식(differential equation)의 일종이다.
'Audio' 카테고리의 다른 글
| 오디오 스펙의 허상 SNR (신호대잡음비) - LP와 CD (0) | 2024.02.29 |
|---|---|
| 오디오 스펙의 허상 Frequency Range (주파수 대역) 20 ~ 20,000 Hz (0) | 2024.02.29 |
| 음악과 물리학 – 3. 피아노 해머 (0) | 2024.02.29 |
| 음악과 물리학 - 2. 소리와 파동 (0) | 2024.02.29 |
| 음악과 물리학 – 1. 악기 분류법 (0) | 2024.02.29 |




