오디오를 하다 보면 현실적인 난제에 부딪힐 때가 한두 번이 아닙니다. 이 스피커에 어느 정도 출력의 앰프를 물려도 되는지, 오디오 전원을 켜고 끌 때 특별한 순서가 있는지, 포노 카트리지의 고출력과 저출력을 나누는 기준점은 무엇인지 등등이죠.
또한 알아두면 언제든 유용하게 쓸 수 있는 팁도 제법 많습니다. 임피던스 매칭 기본 원칙은 '작게 주고 크게 받는다', 감도가 3dB 낮은 스피커에서 동일한 음량을 얻으려면 앰프 출력은 2배가 되어야 한다, 낮은 음량에서는 저역이 잘 안 들린다 등이 대표적입니다.
하이파이클럽에서 이 같은 현실적 고민과 솔루션, 실용적인 오디오 팁을 모아 새 연재물 [오디오 룰 오브 썸]을 시작합니다. '룰 오브 썸'(Rule Of Thumb)은 엄격하고 복잡한 수식이나 법칙이 아나라 일반적으로 통용되는 간편하고 알기 쉬운 법칙을 뜻합니다. '엄지손가락의 법칙'이라고 이름이 붙은 것은 예전 엄지손가락을 이용해 물건의 길이를 쟀던 데에서 유래됐습니다.
오디오 룰 오브 썸 No.1 :
100W RMS 스피커에는 160W~250W 앰프가 마지노선

많은 애호가들이 맞닥뜨리는 고민 중 하나는 '과연 이 스피커에 출력이 어느 정도 되는 앰프를 물려야 하나?'다. 이 같은 고민에는 너무 센 출력의 앰프를 연결했을 때 스피커가 고장 나지 않을까 하는 두려움이 도사리고 있다. 예를 들어 스피커 스펙에 앰프 허용 입력(power handling)이 '100W RMS(Root Mean Square)' 또는 '정격 100W' 또는 영어로 ' Continuous 100W'라고 돼 있는 경우, 300W RMS 출력 앰프를 물리면 어떻게 될까.
이처럼 스피커와 앰프 매칭이 고민될 때 유용한 룰 오브 썸이 있다.
앰프 출력 = 최저 : 스피커 앰프 허용 입력(W RMS) x 2 x 0.8, 최대 : 스피커 앰프 허용 입력(W RMS) x 2 x 1.25
또는 '스피커 RMS 출력에 2를 곱한 후 80~125% 사이의 앰프를 선택하면 된다'로 기억하면 된다.

예를 들어 공칭 임피던스 8옴 스피커의 앰프 허용 입력이 100W RMS이라면, 8옴에서 160W(200 x 0.8)~250W(200 x 1.25) RMS 출력을 내는 앰프를 물려줘도 스피커에는 아무런 문제가 발생하지 않는다. 200W RMS라면, 320W~500W RMS 출력의 앰프를 매칭하면 된다.
그런데 이러한 파워핸들링, 또는 파워레이팅(Power Rating) 표기 대신에, '권장 앰프 출력(Recommended Amplifier) 160W~250W' 등으로 표기하는 스피커도 많다. 이는 스피커의 안전과 함께 최적의 음질을 확보할 수 있는 앰프 출력이라는 뜻이다.
흔히 앰프 출력이 스피커 허용 입력을 넘어갈 때만 문제가 생기는 것으로 생각할 수 있지만, 출력이 부족한 앰프도 스피커에 치명상을 입힌다. 앰프의 과다 출력(+높은 볼륨)은 스피커 보이스코일에 높은 열을 발생시켜 문제가 되고, 출력이 지나치게 낮은 앰프는 쉽게 클리핑을 일으킬 수 있기 때문에 스피커에도 고주파수 처리 및 발열 등의 문제를 일으키게 된다. 스피커 스펙에 '권장 앰프의 최소 입력'이 표기되는 것은 음질과도 관련이 있지만 이 같은 스피커 자기 보호 이유도 크다.
참고로 최근 필자가 리뷰한 몇몇 스피커의 앰프 허용 입력 표기는 다음과 같다.
모니터오디오 Gold 200 : 파워핸들링 200W RMS
JBL 4306 : 파워핸들링 150W RMS
파인오디오 F1-8 : 파워핸들링 90W RMS
탄노이 Stirling GR : 파워핸들링 85W RMS
탄노이 Canterbury GR : 파워핸들링 125W RMS (550W Peak)
다인오디오 Confidence 20 : 파워핸들링 250W (RMS)
다인오디오 Confidence 50 : 파워핸들링 400W (RMS)
다인오디오 Confidence 60 : 파워핸들링 600W (RMS)
B&W 802 D3 : 권장 앰프출력 50W~500W into 8ohms
B&W 800 D3 : 권장 앰프출력 500W~1000W into 8ohms
매지코 A3 : 권장 앰프출력 50W~300W RMS
매지코 A5 : 권장 앰프출력 50W~1000W RMS
로저스 LS3/5a : 권장 앰프출력 30W~80W
윌슨베네시 Eminence : 최소 권장 앰프출력 100W
타이달 Contriva G2 : 최소 권장 앰프출력 30W

왼쪽부터 JBL 4306 스피커, Fyne Audio F1-8 스피커
JBL 4306 스피커의 경우 허용 입력이 150W RMS이기 때문에 선택 가능한 앰프의 최대 출력 마지노선은 240W~375W RMS가 된다. 파인오디오 F1-8 스피커의 경우 허용 입력이 90W RMS이기 때문에 144W~225W RMS 출력의 앰프가 마지노선이다.

Tannoy Canterbury GR-OW 스피커
이에 비해 탄노이 캔터베리 GR 스피커는 RMS와 피크 출력을 모두 표기해 눈길을 끈다. 125W RMS를 기준으로 하면 매칭 가능한 앰프의 최대출력은 RMS 기준 200W~312.5W, 피크 출력 기준 400W~625W가 된다. 그러나 제작사에서 밝힌 피크 출력이 550W이므로, RMS 기준 200W~275W 앰프가 상한선이 된다.

왼쪽부터 B&W 800 D3 스피커, Magico M2 스피커
한편 B&W 800 D3나 매지코처럼 최소와 최대 권장 앰프 출력을 표기한 스피커는 앰프 출력(RMS)이 해당 범위 안에 있을 때 스피커 안전은 물론 최적의 음질을 낼 수 있다는 뜻이다. 따라서 800 D3의 경우 8옴에서 50W~1000W를 내는 앰프가 음질 면에서 가장 좋다는 뜻이지, RMS 출력이 1000W를 넘기는 앰프에 물리면 안 된다는 뜻은 아니다.
그러면 'x2 x 0.8 ~ x2 x 1.25'라는 룰 오브 썸은 어떻게 나온 것일까.
우선 스피커에서 100W RMS라고 밝혔는데도 왜 2를 곱하는지부터. 이는 앰프가 사인파(sine wave)를 기준으로 RMS 출력을 계산하는데 비해, 스피커는 핑크 노이즈(pink noise)를 테스트 신호로 삼기 때문이다. 사인파는 피크 전압이 RMS 전압에 비해 1.41배(3dB) 높고, 핑크 노이즈는 피크 전압이 RMS 전압에 비해 4배(12dB) 높다. 이를 보여주는 것이 아래 두 그래프다.
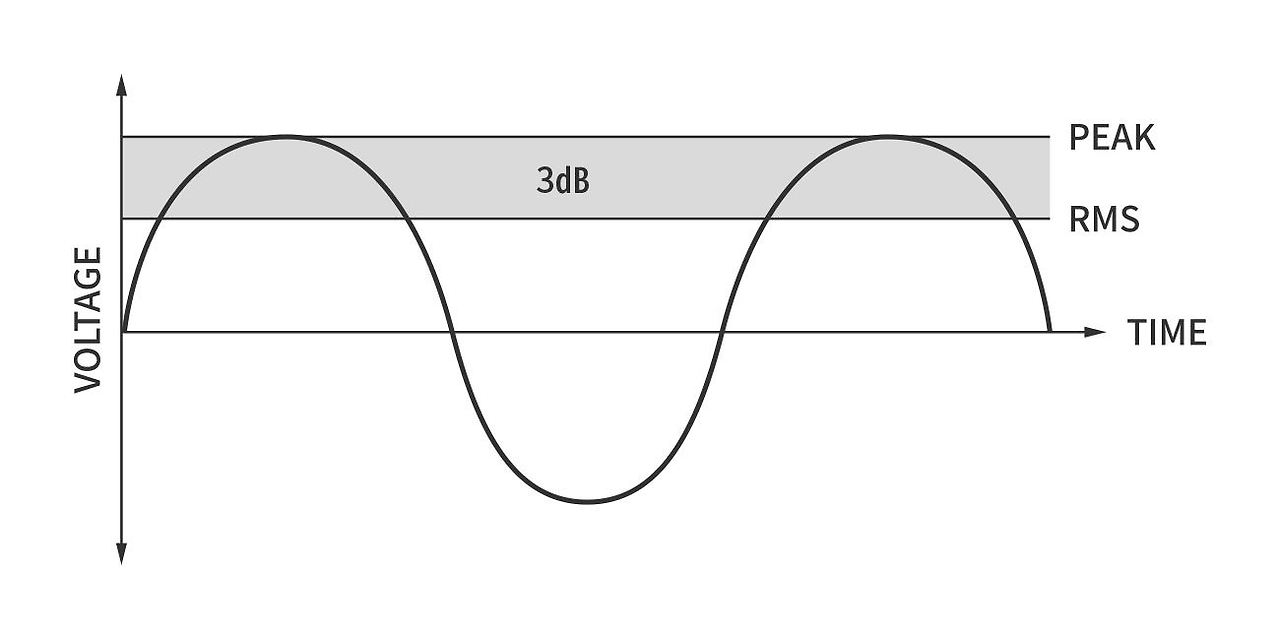
사인파의 RMS 전압과 피크 전압
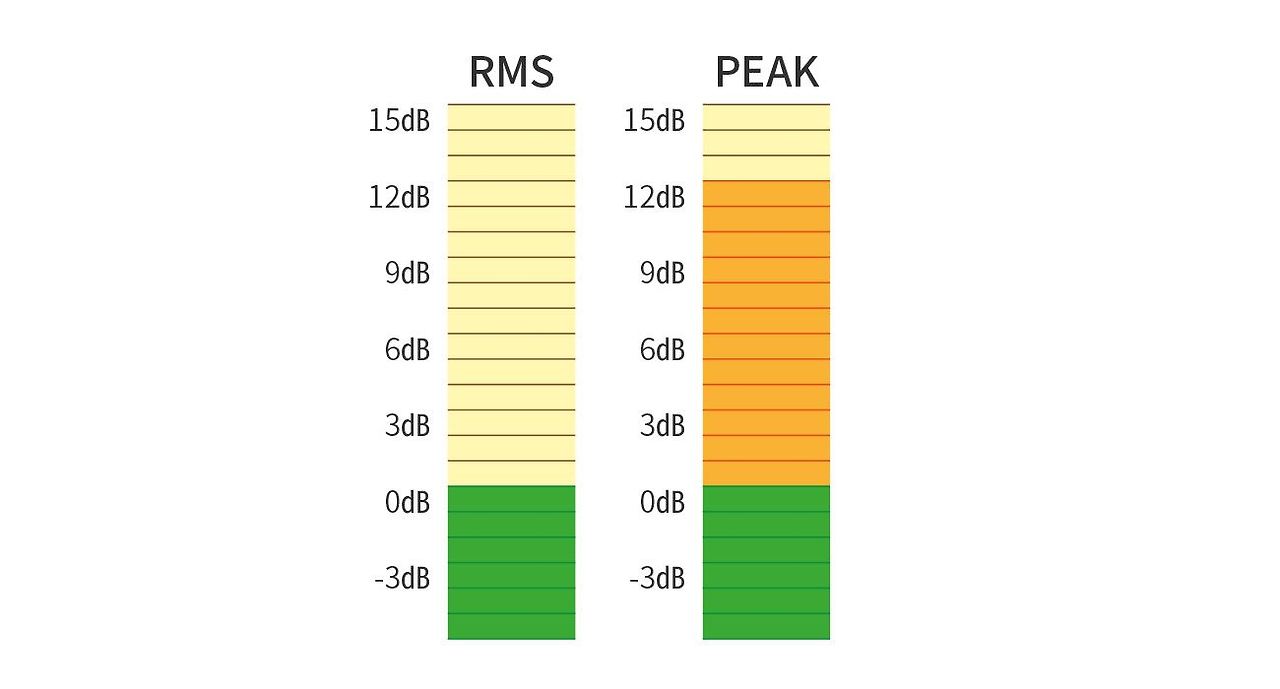
핑크 노이즈의 RMS 전압과 피크 전압
그런데 출력, 즉 전력을 기준으로 환산하면, 사인파의 피크 출력이 RMS 출력보다 2배(3dB), 핑크 노이즈의 피크 출력이 RMS 출력보다 4배(6dB) 높게 된다. 앰프 허용 입력이 100W RMS인 스피커는 핑크 노이즈의 순간 피크 출력값이 400W라는 얘기가 된다. 결국 이 스피커는 피크 출력값이 400W, RMS 출력값이 200W인 앰프에 물려도 된다. 그래서 스피커의 허용 입력 100W에 2를 곱하게 된 것이다.
| Clinical Range | ± In(ratio) | Acceptable Range |
| ± 20% | ± 0.223 | 80 - 125% |
| ± 30% | ± 0.357 | 70 - 143% |
| ± 50% | ± 0.693 | 50 - 200% |
+,-20% 생물학적 등가성 원칙
그러면 '80~125%' 값은 도대체 어디서 왔고, 왜 '80~120%'이 아닌 걸까. 이 특정 범위를 처음 주장한 사람은 미국 스피커 제작사 EAW의 수석 엔지니어 척 맥그레거(Chuck McGregor)로, '+,- 20% 오차 범위는 임상적으로 차이가 없다'라는 미국 FDA 기준(생물학적 등가성 원칙. Bioequivalence Criteria)에서 차용한 것으로 알려졌다. 즉, RMS 출력이 딱 100% 맞아떨어지는 앰프가 아니더라도 80~125% 출력의 앰프라면 실용상 차이가 없다는 뜻이다.
주의할 점은 +20%와 -20%가 자연로그 값을 기준으로 한다는 것. 이들을 자연로그 값으로 표기하면 각각 0.223과 -0.223이 되고, 이를 다시 십진법 퍼센트로 표기하면 각각 80%와 125%가 된다. 그래서 예를 들어 200 W RMS에 각각 0.8과 1.25를 곱하는 것이다. 마찬가지로, +30%와 -30%를 자연로그 값으로 표기하면 각각 0.357과 -0.357이 되고 이에 대한 각각의 십진법 퍼센트는 각각 70%와 143%가 된다.
'Audio' 카테고리의 다른 글
| 오디오를 세정해야 하는 이유,전자파 & 고조파 노이즈 (0) | 2024.02.29 |
|---|---|
| 백지에서 시작하는 델타 시그마 DAC (0) | 2024.02.29 |
| 케이블 이야기 2 - 케이블 전도도와 외부환경 (1) | 2024.02.29 |
| 케이블 이야기 1 - 케이블이 소리를 좋게 하지 않습니다. 나쁜 영향을 주지 말아야 합니다. (1) | 2024.02.29 |
| 말도 많고 탈도 많은 디지털 - 디지털이 뭐길래 (0) | 2024.02.29 |




